Lesson 5: Expanding Brackets

Objective

At the end of this lesson, students should be able to:

• Expand products of algebraic expressions.

Expanding an expression means writing it without brackets. When removing brackets, every term inside the bracket must be multiplied by whatever is outside the bracket.

Directed numbers are numbers with either a positive or a negative sign. When using these numbers in algebra, it is important that we follow the same rules as we would for normal directed number calculations.

(Positive number)   × / ÷ (Positive number) = (Positive number)

(Negative number)  × / ÷ (Negative number) = (Positive number)

(Positive number)  × / ÷ (Negative number) = (Negative number)

(Negative number)  × / ÷ (Positive number) = (Negative number)

So 8  (– 3y) = – 24xy and (– 8  (– 3y) = 24xy

Example 1

Expand the algebraic expression.

Solution

Example 2

Expand the algebraic expression.

Solution

Example 3

Expand the algebraic expression:

Solution

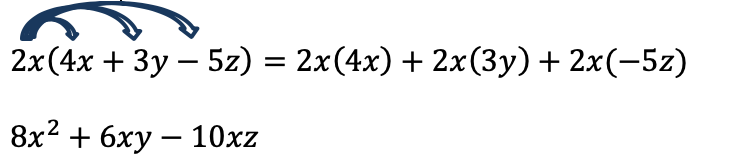
Example 4

Expand the algebraic expression – 4x ( x – y + z²).

Solution

– 4x (x – y + z²)

– 4x (x) – 4x(–  y) – 4x (z²)

– 4x² + 4xy – 4xz²

Example 5

Expand the algebraic expression: – 2a² (a + 3b – ¹/_a).

Solution

– 2a² (a + 3b – ¹/_a)

– 2a²(a) –  2a²(3b) – 2a² (– ¹/_a)

–  2a³ – 6a²b + 2a

Example 6

Expand the algebraic expression – ²/_x (– x + 4y + 1/x).

Solution

– ²/_x – (x + 4y + 1/x)    =  – ²/_x (– x) – ²/_x (4y) – ²/_x (¹/_x)

= 2 – ^8y/_x – ²/x²